梯度下降是机器学习中非常流行的一种优化算法,在神经网络中更是最常用的一种方法。与此同时,也产生了大量的变种和改进的算法,这些算法在caffe、keras等等深度学习框架中被大量采用和实现。本篇主要介绍不同变种的梯度下降。
目录
之前,看到过的一篇英文博客An overview of gradient descent optimization algorithms。前一段时间,在写属于自己的工具箱kitnet中,实现了一些基本的优化算法,参考了这篇博客,后来其他一些事情,中间隔了不少时间,没有好好的把梯度下降整理完,先给出第一部分吧。
梯度下降是机器学习中非常流行的一种优化算法,在神经网络中更是最常用的一种方法。与此同时,也产生了大量的变种和改进的算法,这些算法在caffe、keras等等深度学习框架中被大量采用和实现。本篇主要介绍不同变种的梯度下降。
SGD
对于优化的目标函数\(J(\theta)\),参数\(\theta \in R^d\), 我们要使用的梯度为\(\nabla _\theta J(\theta)\),学习速率为\(\eta\),最常见是batch gradient descent(BGD,批量梯度下降),更新公式如下: \(\theta := \theta - \eta \nabla _\theta J(\theta)\)
上面的batch是等于所有训练样本数。当batch数等于1的时候,就是随机梯度下降(Stochastic gradient descent (SGD)),也可以称之为online 随机梯度下降。更新公式和伪代码如下: \(\theta := \theta - \eta \nabla _\theta J(\theta;x^{i},y^{i})\)
当batch数小于整体样本数,大于1的时候,更新称之为mini-batch梯度下降。batch指得就是每次梯度更新时,所使用的样本数。样本数越多,那么计算的J就越接近全局的J,更新的梯度就越准确,相反batch数很小,会导致某些更新是局部较优而整体不优的情况。但是,当J存在多个局部最优解的时候,较小的batch可能会让你在某次更新中跳过某些局部最优解。 给一下mini-batch的伪代码:
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
SGD的问题
对于mini-batch梯度下降,并不能很好得保证收敛,存在一些挑战:
- 需要选择一个合适得学习速率;学习太小,导致更新太慢、耗时;学习速率太大,可能会导致loss在最优解附近波动而不收敛。
- 虽然可以设计一些学习速率的变化方式,比如模拟退火等思路,比如更新到一定程度了就线性的减小学习速率等等,都需要预先定义一些东西,而且在不同得场景下,需要各种尝试;
- 有些学习速率是对于所有得参数都是一样。如果我们得参数是稀疏的,而且特征的频度差距比较大,我们可能会希望对于出现次数较少的特征,每次学习速率稍微大一点。
- 另外一个比较关键的挑战是对于非凸优化(比如神经网络)的误差函数而言,如何避免局部最优解,尤其是马鞍点(因为梯度十分接近0)
下面分别介绍一些变种。
Momentum
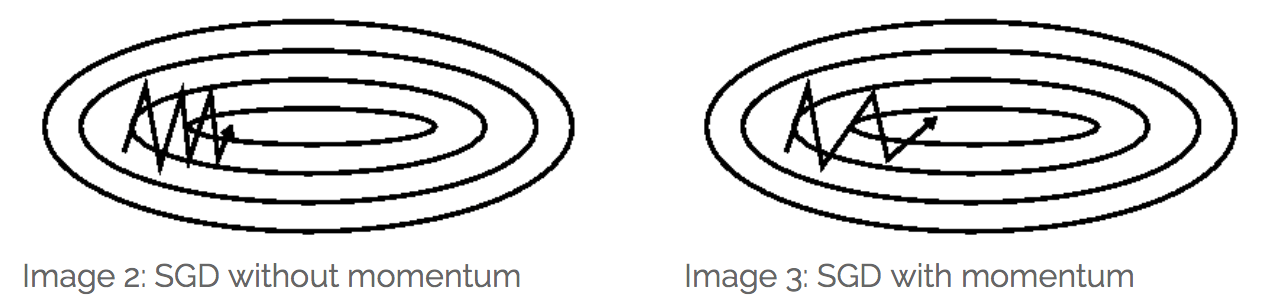
SGD很难穿越一些梯度沟壑(ravines,即在某个方向上得梯度远大于其他方向,参考 Sutton, R. S. (1986): Two problems with backpropagation and other steepest-descent learning procedures for networks ).如下图所示:
引入Momentum(动量)之后更新变为:
\(v_t = \gamma v_{t-1} + \eta \nabla _\theta J(\theta)\) \(\theta := \theta - v_t\) 直观的理解是抛一个小球下山,小球在下山过程中会不断的加速,在同一个方向上,越来越快。
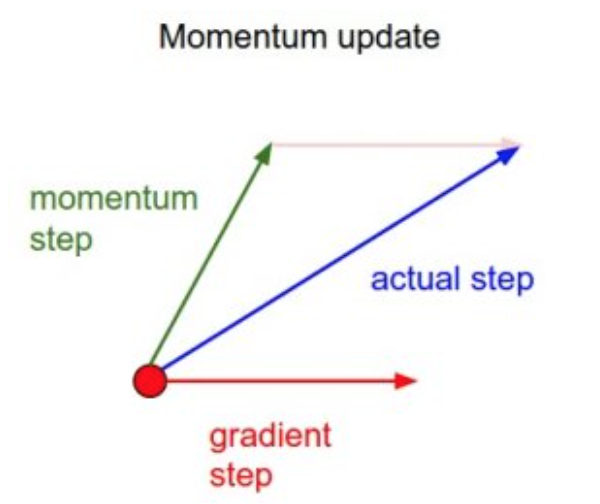
如上图所示,momentum项增加了更新的梯度方向与之前是同一个方向的更新量(With Momentum update, the parameter vector will build up velocity in any direction that has consistent gradient.),比如说,对于某些参数,这次的更新和上次的更新方向一直相同,那这个梯度方向应该比较正确得方向,那么更新量会变大。相反,对于某些参数,前后梯度更新的方向发生变化,很可能是因为之前更新量大了,所以在这一次更新中会减少更新量,从而使得我们得收敛变快,减少了摆动。 一般而言,在刚开始的更新阶段,梯度都比较大,\(\gamma\)可以设置的小一点,比如0.5,这样每次更新更多的依赖当前的梯度。随着更新的不断进行,我们可以设置为0.9或者0.99等。
Nesterov accelerated gradient
Nesterov accelerated gradient (NAG)是在动量之上的又一个改良,他给了我们得动量项某种预知能力。之前,我们使用\(\gamma v_{t-1}\)来更新\(\theta\),那么提前计算\(\theta - \gamma v_{t-1}\),可以估计出参数的下一个位置。因此,可以提前计算出下一步的梯度,用于这一步的更新(相当于一次更新两步),如下: \(v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta-\gamma v_{t-1})\) \(\theta := \theta - v_t\) 如果我们得\(\gamma\)设为0.9,当第一次计算当前梯度的时候,如下图绿色得向量。红色的是我们提前计算的梯度,加起来得到实际的梯度,这个过程避免了本次更新走得歪路,强化了正确的部分(向量想加的更新思路,类似于感知机的学习思路)
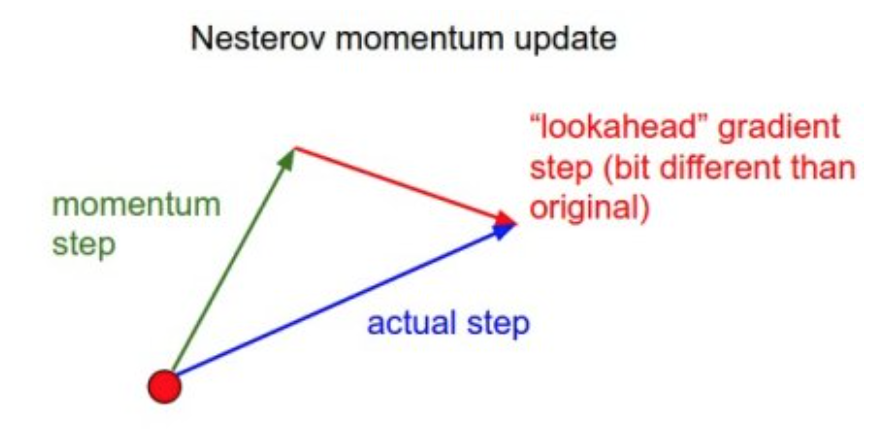
这种方法在RNN等多种任务表现非常好,而且收敛速度加快。
Adagrad
Adagrad的思路是基于:针对于每一个参数都有他自己的学习速率,对于不常出现的参数,每次更新大一点;对于经常出现得参数,每次更新小一点。这种优化算法,在稀疏矩阵中应用比较多。Dean等人在Large Scale Distributed Deep Networks中指出,Adagrad非常大的提升了SGD的鲁棒性,并用于训练大规模神经网络。详细,可以看参考论文。 之前的更新思路,对于所有的参数\(\theta\)的一次更新都是共用一个学习速率\(\eta\)。下面,先给出Adagrad每一个的参数更新公式,为了方便,我们定义\(g_{t,i} = \nabla_ \theta J(\theta_i)\),那么正常的SGD更新参数方式如下: \(\theta_{t+1, i} := \theta_ {t,i} - \eta g_{t,i}\) 根据这个更新规则,Adagrad的做法是,每次根据该参数\(\theta_i\)过去计算的梯度来修正学习速率\(\eta\),那么可以更新公式为:
\[\theta_{t+1, i} = \theta_{t, i} - \frac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i}\]\(G_{t} \in \mathbb{R}^{d \times d}\)是一个对角矩阵,对角上的值是累计到更新次数t时的 梯度的平方和,\(\epsilon\)一般设置为1e-8,避免分母是0;此外,如果没有开方操作,效果会非常差! 因为\(G_t\)中包含了所有参数的累积梯度,那么参数更新可以用矩阵形式表达如下(注意:\(\odot\)表示element-wise的乘法):
\[\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{G_{t} + \epsilon}} \odot g_{t}\]Adagrad的好处之一是不用手动去调整学习速率。多数实现,都是设定默认值为0.01,之后让它自己变。它的主要不足就是需要不断的累计计算分母上的梯度平方,因为平方都是正向,所以这个值也是不断的在增加,可能会出现学习速率变小到无限小,导致模型无法更新了。对于类似于的一些模型,可以参考FTRL。
Adadelta
Adadelta是Adagrad的一种扩展,用于避免比较激进的单调递减的学习速率。Adadelta采用一个窗口来限制过去梯度的累积来更新w,而不是像Adagrad那样用过去所有的梯度累计。
Adadelta不再是存储之前梯度平方和,而是在更新t次时,计算均值\(E[g^2]_t\)时仅依赖于上次的这个均值和当前的梯度,更新公式如下: \(E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t\) 实际的参数更新类似于Agagrad,我们用\(E[g^2]_t\)来代替对角矩阵\(G_{t}\),公式为:
\[\Delta \theta_t = - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}\]为了方面查看,我们将公式改写如下:
\[\Delta \theta_t = - \frac{\eta}{RMS[g]_{t}}\]从上式子可以看到一个现象(SGD,Momentum,Adarad都存在这个问题):参数更新过程中,左右单位不一致。(注:\(\Delta x 的单位 \propto g的单位 \propto \frac{\partial f}{\partial x} \propto \frac{1}{x的单位}\))。为了解决这个问题,现在再定义一个指数衰减,这一次不使用梯度平方,而是使用参数更新量的平方:
\[E[\Delta \theta ^2]_t = \gamma E[\Delta \theta ^2]_{t-1} + (1-\gamma)E[\Delta \theta ^2]_t\]那么参数更新的RMS为:
\[RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon}\]实际上\(RMS[\Delta \theta]_t\)是未知的,我们可以用上一次的值来近似他,之后替换掉学习速率\(\eta\),得到最后的更新公式:
\[\Delta \theta_t = - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t}\]RMSprop
RMSprop并未正式的发布,由Geoff Hintion在公开课中提及。RMSprop和Adadelta均是用于解决Adagrad中学习速率迅速减小的问题。 RMSprop等价于Adadelta中的一种情况: \(E[g^2]_t = 0.9E(g^2)_{t-1} + 0.1 g^2_t\) \(\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}}\)
RMSprop也除以一个指数衰减的平均梯度和,Hiton建议\(\gamma\)设置为0.9,初始学习速率\(\eta\)设置为0.001
Adam
Adaptive Moment Estimation (Adam) 是另外一种自适应的计算各个参数的学习速率的方法。除了计算过去梯度平方和的指数衰减之外,adam还增加了一项过去梯度平均的指数衰减,类似于momentum,即
\[m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t\] \[v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2\]这里的\(m_t\)和\(v_t\)是梯度的一阶(均值)和二阶(方差)的估计值,这些值一般初始化设置为0.但是这些值收到\(\beta\)的影响而变得有偏,一般修正如下:
\[\hat{m_t} = \frac{m_t}{1- \beta^t_1}\] \[\hat{v_t} = \frac{v_t}{1- \beta^t_2}\]之后的参数更新类似于Adadelta和RMSprop: \(\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}} + \epsilon} \hat{m_t}\)
一般建议 \(\beta_1 =0.9, \beta_2=0.999,\epsilon=10^{-8}\)。经验表明,Adam在这些自适应学习速率的方法表现较好~