该部分主要是复习一下机器学习概率分布的相关知识。这里的概率分布主要讲两个方面：其一是密度估计(Density Estimation)，主要是频率学派和贝叶斯学派的方法。其次是共轭先验，主要是方便后验概率计算。本笔记分上下两个部分，第一部分是这里的各个分布概述；第二部分是指数族分布和非参数估计。这一篇记录第一部分。

注：本文仅属于个人学习记录而已！参考Chris Bishop所著Pattern Recognition and Machine Learning(PRML)以及由Elise Arnaud, Radu Horaud, Herve Jegou, Jakob Verbeek等人所组织的Reading Group。

目录

• 1.二元变量
• 2.多元变量
• 3.高斯分布
  • 3.1高斯分布基础
  • 3.2条件高斯分布
  • 3.3最大似然
  • 3.4贝叶斯
  • 3.5局限性
• 4.其他分布

1.二元变量

首先是对于二元变量(Binary Variables)， \(x \in {0,1}\) ,参数 \(\mu\) , \(p(x)\) 满足 \(p(x=1 \mid \mu)=\mu, p(x=0 \mid \mu) = 1-\mu\) ，那么我们称\(p(x)\)是伯努利分布(Bernoulli distribution)，表示如下：

\[Bern(x \mid \mu) = \mu^x(1-\mu)^{1-x}\]

那么我们如何估计参数\(\mu\)呢？首先是使用频率学派(Frequentist’s Way)的方法，即采用最大似然估计(maximum likelihood estimate)，假设各次观测独立同分布的，我们可以得到：\(\mu^{ML} = \frac{m}{N}\) ,这里m是观测值中\(x=1\)出现的次数。这种观点很容易导致过拟合(overfitting)，尤其是在观测数N比较小的时候，比如独立投掷硬币3次，均出现正面向上，即 N=m=3，那么 \(\mu^{ML} = 1\)，很可能不合符实际常识。

我们考虑采用贝叶斯学派(Bayesian Way)的方法。贝叶斯学派关注事情是如何发生的，而不仅仅是发生的结果。在使用贝叶斯方法之前，先介绍两个分布。对于二元变量(Binary Variables) \(x \in {0,1}\) ，这里采用了二项分布(binomial distribution describes)，即描述包含N个观测值的数据集中，\(x=1\)观测值出现次数m的分布，即：

\(Bin(m \mid N,\mu) = {N \choose m} \mu^m(1-\mu)^{N-m}\)，其中 \({N \choose m} = \frac{N!}{(N-m)!m!}\)

为了方便计算，选择先验分布为Beta分布，

\(Beta(\mu \mid a,b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}\)，其中\(\Gamma(x) = \int_0^\infty \mu^{x-1}e^{-\mu}d\mu\)

Gamma函数是实数阶乘的拓展，即\(\Gamma(n) = (n-1)!\)，参数a和b控制着概率密度函数的形状，两者都必须是正值，在这里称之为超参数(hyperparameters), 控制着参数\(\mu\)的分布。对于Beta分布的均值和方差分布如下：

\[E(\mu) = \frac{a}{b} \ \ \ ; \ \ \ var[\mu] = \frac{ab}{(a+b)^2(a+b+1)}\]

根据贝叶斯公式，我们可以得到\(p(\mu \mid m,l,a,b) \propto Bin(m,l \mid \mu)Beta(\mu \mid a, b)=\mu^{m+a-1}(1-\mu)^{l+b-1}\), 这里l = N - m。最终得到：

\[p(\mu \mid m,l,a,b) = \frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1}\]

从这里可以看出：x=1和x=0的实际观测数是m，l，而得到的后验概率中a增加了m，b增加了l，可以简单的认为超参数a和b是有效观测次数。在观测数据iid(Independent Identically Distributed, 独立同分布)的假设下，随着观测数据的不断增加（sequential approach），不断的修正着超参数a和b，即实际观测不断的修正着先验认知。

在已经观测数据集D上，如果新来了一个数据x，那如何预测呢？即判断x=1的概率。

\[p(x=1 \mid D) = \int_0^1 p(x=1 \mid \mu)p(\mu \mid D)d\mu = \int_0^1 \mu p(\mu \mid D)d\mu = E(\mu \mid D) = \frac{m+a}{m+a+l+b}\]

我们注意到当观测值ml不断增大到可以忽略ab时，参数均值会收敛到最大似然的结果。即大量数据下，贝叶斯和频率学派的结果是一致的。同时也能看出了，观测数据不断上升时，参数的方差也在减小。

拓宽来说，对于普通的贝叶斯推断问题，参数\(\theta\)，考虑到条件期望和条件方差，我们可以推导：

\[\begin{align} E_D[E_\theta[\theta \mid D]] &= \int{(\int{\theta p(\theta \mid D) d\theta}) p(D)}dD \\ &= \int{(\int{p(\theta \mid D) p(D) dD})\theta d\theta} \\ &= \int{p(\theta)\theta d\theta} \\ &= E_\theta(\theta) \end{align}\] \[\begin{align} var_\theta[\theta] &= E_\theta[\theta^2] - [E_\theta[\theta]]^2 \\ &= E_D[E_\theta[\theta^2 \mid D]] - [E_D[E_\theta[\theta \mid D]]]^2 \\ &= E_D[E_\theta[\theta^2 \mid D]] - E_D[E_\theta[\theta \mid D]^2] + E_D[E_\theta[\theta \mid D]^2] - [E_D[E_\theta[\theta \mid D]]]^2 \\ &= E_D[var_\theta[\theta \mid D]] + var_D[E_\theta[\theta \mid D]] \end{align}\]

由此看出参数后验概率的方差是小于先验概率方差的，即参数的不确定性随着观测数据而降低。当然，这只是理想情况，实际过程中，也存在大于的情况。

2.多元变量

对于多元变量(Multinomial Variables)，假设随机变量有K个互斥状态(mutually exclusive states)，用K维度的向量x表示，对于状态K发生时，\(x_k=1, x_{i \neq k} =0\)。那么对于伯努利分布可以扩展为 \(p(x \mid \mu) = \prod_{k=1}^{K}\mu_k^{x_k}\)，这里要求\(\sum_k\mu_k = 1\)。

对于有N个独立观测的数据集D，使用最大似然估计，可以得到：

\[p(D \mid \mu) = \prod_{n=1}^N \prod_{k=1}^K \mu_k^{x_nk} = \prod_{k=1}^K \mu^{\sum_n x_{nk}} = \prod_{k=1}^K \mu_k^{m_k}\]

取对数，并且结合\(\sum_k\mu_k = 1\)，使用拉格朗日法，得到\(L(\mu) = \sum_{k=1}^K m_k \ln \mu_k + \lambda (\sum_{k=1}^K \mu_k -1)\)，得到\(\mu_k = \frac{-m_k}{\lambda}\)，最后估计值为 \(\mu^{ML} = \frac{m_k}{N}\)。

多项分布(multinomial distribution)是二项分布的扩展，即是上面提到的各个\(m_k\)的分布，形式如下：

\[Mult(m_1,...,m_k \mid \mu,N) = {M \choose {m1...m_k}} \prod_{k=1}^K \mu_k^{m_k} \ \ \ ; \ \ \ {M \choose {m1...m_k}} = \frac{N!}{m_1!...m_k!}\]

注意这里存在一个约束\(\sum_{k=1}^K m_k = N\)。

现在我们考虑贝叶斯方法。采用狄利克雷分布(Dirichlet distribution)作为共轭先验，形式如下：

\[Dir(\mu \mid \alpha) = \frac{\Gamma(\alpha_0)}{\Gamma(\alpha_0)...\Gamma(\alpha_K)} \prod_{k=1}^K \mu_k^{\alpha_k-1} \ \ \ ; \ \ \ \alpha_0 = \sum_{k=1}^K \alpha_k\]

接下来用先验概率乘以似然函数，得到后验分布： \(p(\mu \mid D,\alpha) \propto p(D \mid \mu)p(\mu \mid \alpha) \propto \prod_{k=1}^K \mu_k^{a_k+m_k-1}\) \(p(\mu \mid D,\alpha) = Dir(\mu \mid \alpha+m) = \frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1) ...\Gamma(\alpha_k+m_k)} \prod_{k=1}^K \mu_k^{a_k+m_k-1}\)

类似于beta分布，我们也可以认为\(a_k\)是\(x_k=1\)的有效观测数。

3.高斯分布

3.1高斯分布基础

对于x是D维度的高斯分布(The gaussian distribution)形式为：

\[N(x \mid \mu,\Sigma) = \frac{1}{(2\pi)^{D/2} {\mid \Sigma \mid}^{1/2}} exp(-\frac{1}{2}(x-\mu)^T \Sigma^{-1} (x-\mu))\]

我们可以从很多角度思考高斯分布，比如最大熵、中心极限定理等思考角度。高斯分布是非常基础和核心的一个分布，所以这部分相对讲的比较多一些，用到很多矩阵的知识。但是，高斯分布是值得付出这么学习的。

高斯分布的一些属性如下：

• x的期望：\(E(x) = \mu\)
• x的方差：\(cov(x) = \Sigma\)

此外，我们考虑高斯分布的几何特性。首先x到\(\mu\)的马氏距离(Mahalanobis distance)是\(\Delta^2 = (x-\mu)^T\Sigma^{-1}(x-\mu)\)，是高斯分布的函数依赖(functional dependence),即给定这个二次型(quadratic form)，高斯分布就被决定下来了。 \(\Sigma\)是对称矩阵(symmetric matrix)，他的特征向量U是正交的。定义\(y = U(x-\mu)\)，那么上面的二次型可以用如下等高线图表示：

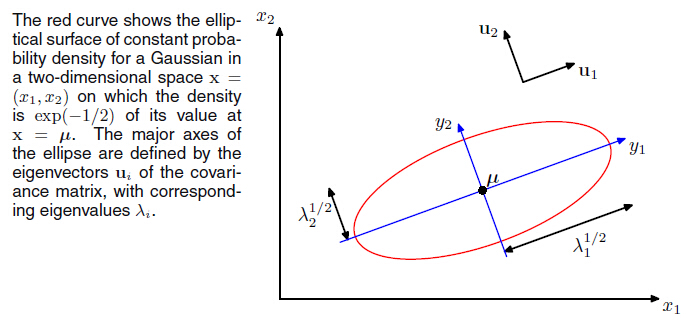
其中，\(\lambda_i\) 是\(\Sigma\)的特征值， \(u_i\)是对应的特征向量。这里我们提及行列式的一个性质\(\mid \Sigma \mid = \prod_{j=1}^D \lambda_j^(\frac{1}{2})\)。高斯分布是最常使用的概率密度，但是通常会有一些限制。因为正常情况下高斯分布含有 D(D+1)/2 + D 个独立参数，即是随着维度增长而二次增长。因此，有时候我们会限制\(\Sigma\)是对角矩阵(即属性间相互独立，等高线图中特征向量与属性是平行的)，有时候会限制\(\Sigma\)是单位矩阵(等高线图是一个个圆)。书中还简介了一些以后会深入讲的一些东西，比如潜在变量模型、图模型等。

3.2条件高斯分布

多元高斯分布的一个重要性质是：如果两组变量联合分布是高斯分布，那么一组变量基于另一组变量的条件分布也是高斯分布。类似的，每组变量的边际分布也是高斯分布。即对于高斯分布 \(N(x \mid \mu, \Sigma)\)，考虑分割成a和b的联合分布，即

\[x = (x_a,x_b)^T \ \ \ ; \ \ \ \mu = (\mu_a,\mu_b)^T\] \[\Sigma = \begin{pmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix}\]

那么条件分布\(p(x_a \mid x_b)\)是高斯分布，参数为：\(\mu_{a \mid b} = \mu_a + \Sigma_{ab} \Sigma_{bb}^{-1} (x_b - \mu_b) \ \ \ ; \ \ \ \Sigma_{a \mid b} = \Sigma_{aa} - \Sigma_{aa} \Sigma_{bb}^{-1} \Sigma_{ba}\)； 边际分布\(p(x_a)\)也是高斯分布，参数是\((\mu_a, \Sigma_{aa})\)。推导蛮复杂的，可以看参考书本。

考虑高斯模型，对于x是高斯分布，即\(p(x) = N(x,\mu,\Lambda), p(y \mid x) = N(y,Ax+b, L^{-1})\)，其中\(y = Ax + b + \epsilon\)， 那么有：

\(p(y) = N(y, A \mu + b, L^{-1}+A \Lambda A^T)\) \(p(x \mid y) = N(x \mid \Sigma(A^TL(y-b) + \Lambda\mu), \Sigma) \ \ \ ; \ \ \ \Sigma = (\Lambda + A^TLA)^{-1}\)

3.3最大似然

接下来就是如何根据观测数据来进行参数估计了。假设我们有N个服从iid的观测数据，通过对数最大似然估计是：

\[\ln p(X \mid \mu,\Sigma) = -\frac{ND}{2}\ln (2\pi) - \frac{N}{2}\ln \mid \Sigma \mid - \frac{1}{2}\sum_{n=1}^N (x_n-\mu)^T \Sigma^{-1} (x_n - \mu)\]

似然函数的充分统计量(sufficient statistics)是 \(\sum_{n=1}^Nx_n \ \ \ ; \ \ \ \sum\), 之后令参数的偏导数为0，得到结果如下:

\[\mu_{ML} = \frac{1}{N}\sum_{n=1}^N x_n \ \ \ ; \ \ \ \Sigma_{ML} = \frac{1}{N} \sum_{n=1}^N (x_n - \mu_{ML})(x_n - \mu_{ML})^T\]

这里均值的估计是无偏的，但是方差是有偏的，一般会在此基础之上再乘以\(\frac{N-1}{N}\)。此外，我们考虑到on-line的应用(观测数据无法一次整体得到，每次只能使用一个观测)，那么均值的更新方式就需要更改为:

\[\mu_{ML}^N = \frac{1}{N}x_N + \frac{N-1}{N} \mu_{ML}^{(N-1)} = \mu_{ML}^{N-1} + \frac{1}{N}(x_N - \mu_{ML}{(N-1)})\]

这里使用了Robbins-Monro 算法的一个例子。考虑联合分布\(p(z,\theta)\), 定义\(f(\theta) = E(z \mid \theta) = \int zp(z \mid \theta) d \theta\), Robbins-Monro算法的更新机制是

\[\theta^{(N)} = \theta^{(N-1)} + a_{N-1} z(\theta^{(N-1)})\]

把该算法应用在求解最大似然时，只需要代入z就可以，对于高斯分布，\(z = \frac{\partial}{\partial \mu_{ML}} \ln p(x \mid \mu_{ML}, \sigma^2) = \frac{1}{\sigma^2}(x-\mu_{ML})\)。

3.4贝叶斯

用贝叶斯方法进行参数估计，比较复杂,这里先考虑一维的情况。

这里先假设方差已知，均值未知。只有参数\(\mu\)，选择\(p(\mu) = N(\mu \mid \mu_0, \sigma_0^2)\)，那么后验概率是\(p(\mu \mid X) \propto p(X \mid \mu)p(\mu)\)，最终得到\(p(\mu \mid X) = N(\mu \mid \mu_N,\sigma_N^2)\)，其中参数如下:

\(\mu_N = \frac{\sigma^2}{N\sigma_0^2 + \sigma^2}\mu_0 + \frac{N\sigma_0^2}{N\sigma_0^2 + \sigma^2} \mu_{ML}\) \(\frac{1}{\sigma_N^2} = \frac{1}{\sigma_0^2} + \frac{N}{\sigma^2}\)

其中，\(\mu_{ML} = \frac{1}{N} \sum_{n=1}^N x_n\)。可以看到当N趋近于0时，贝叶斯得到的估计结果等于先验的值，而当N趋近于无穷大时，贝叶斯和最大似然得到的结果就一致。同样，当N趋于无穷大时，方差也会趋近于无穷小。

如果均值已知，而方差未知，那么先验分布选择Gamma分布，即取精度\(\lambda = \frac{1}{\sigma^2}\)，则有\(Gam(\lambda \mid a,b) = \frac{1}{\Gamma(a)b^a \lambda^{a-1} exp(-b\lambda)}\)，对于Gama分布，均值为\(\frac{a}{b}\)，方差为\(\frac{a}{b^2}\)。同样代入之后，得到结果如下：

\[p(\lambda \mid X) \propto \lambda^{a_0-1} \lambda^{\frac{N}{2}} exp(-b_0\lambda - \frac{\lambda}{2} \sum_{n=1}^N (x_n - \mu^2)\]

最终得到:

\[a_N = a_0 + \frac{N}{2}\] \[b_N = b_0 + \frac{1}{2}\sum_{n=1}^N(x_n-\mu)^2 = b_0 + \frac{N}{2}\sigma_{ML}^2\]

那么对于均值和方差均未知的情况呢？可以采用normal-gamma分布(也称Gaussian-gamma分布)，即\(p(X \mid \mu,\lambda) = \prod_{n=1}^N (\frac{\lambda}{2\pi})^{\frac{1}{2}} exp(-\frac{\lambda}{2}(x_n - \mu)^2)\), 即\(p(\mu,\lambda) = N(\mu \mid \mu_0, (\beta\lambda)^{-1}) Gam(\lambda \mid a,b)\)

现在我们考虑D维度的问题。如果方差已知，均值未知，那么仍然采用高斯分布；如果均值已知，方差未知，则采用Wishart分布，具体可以参考书本；

3.5局限性

通过以上描述，可以总结出高斯分布的四个不足点：

• 待估计参数太多，有D(D+3)/2；解决方法是简化，比如使用方差选择对角矩阵等；
• 最大似然估计对异常值不鲁棒；解决方法是用t分布或其他分布；
• 无法描述周期函；解决方法是使用von Mises分布
• 是单峰分布；解决方法是使用混合高斯分布；

4.其他分布

对于高斯分布的局限性，我们引入了其他的几个分布，这里简单的概述下；

t分布就是学生分布(t-Student distribution)，是无数多个具体同均值、不同方差的高斯分布的和，对异常值比较鲁棒，函数形式见课本。

当数据具有周期性的时候，有必要采用极坐标(polar coordinates)。而von Mises形式可以参考课本，他的局限性之一也是单峰的，有时候需要使用多个混合。

混合高斯分布是比较重要的分布，在后面也会有混合高斯模型。这里先概述下。它的形式如下：

\[p(x) = \sum_{k=1}^K \pi_k N(x \mid \mu_k, \Sigma_k)\]

其中，\(N(x \mid \mu_k, \sigma_k)\)称之为混合的成分(component)，具有自己的均值\(\mu\)和协方差\(\Sigma_k\)，\(\pi_k\)是混合系数(mixing coefficients)，有\(\sum_{k=1}^K = 1, 0 \le \pi_k \le 1\)。由此，我们联想到概率恰好满足\(\pi_k\)的要求，那么混合高斯概率密度可以写为：\(p(x) = \sum_{k=1}^K p(x)p(x \mid k)\)。具体不再展开，在第九章会具体讲。而对于混合高斯分布的对数似然函数如下:

\[\ln p(X \mid \pi,\mu,\Sigma) = \sum_{n=1}^N \ln (\sum_{k=1}^K \pi_k N(x_n \mid \mu_k,\Sigma))\]

这里明显比单一高斯分布要复杂的多，而且不存在闭合解(解析解)。一般需要使用迭代法(iterative methods)，比如梯度下降、期望最大等等。