本文主要参考Tiny Data, Approximate Bayesian Computation and the Socks of Karl Broman。原作者使用R语言做分析,本文使用Python,且部分参数选择和测试不同。 Approximate Bayesian computation(ABC, 近似贝叶斯计算)是贝叶斯统计的基本方法。
目录
1.问题
虽然我们处在大数据时代,但是有时候你并没有大数据。比如Karl Broman在twitter上的提出一个问题:他在洗衣时候发现11只不同的袜子,请问他实际应该有多少只袜子呢?

如果我们有大量的数据,我们可以用一些机器学习的方法来推断。而目前我们知道的信息有限,因此这里采用了一些统计模型来求解。
2.随机模拟法
我们先考虑这样一个问题,如果已知了实际袜子数(n_socks,比如为18只),从这些中取出11只袜子,看看有多少不同的袜子。这里我们没有直接计算,而是直接使用程序去模拟! 这里我们假设有n_socks=18只袜子,其中有n_pairs=7是成对的,n_odd=4是单只的(遗失4只),从中选n_picked = 11只;首先我们对这18只袜子进行编号,考虑到有成对的袜子,编号socks应该是0-10。程序如下:
n_socks = 18 # The total number of socks in the laundry
n_picked = 11 # The number of socks we are going to pick
n_pairs = 7 # for a total of 7*2=14 paired socks.
n_odd = 4
socks = [i for i in range(7)]*2 + [i for i in range(7,10)]
picked_socks = random.sample(socks, size=min(n_picked, n_socks))
unique_socks = len(set(picked_socks))
pairs = len(picked_socks) - len(set(picked_socks))
那我们可以假设不同的袜子总数,看看结果(这里每个参数,都进行了1w次抽样来平均结果)。这里假设单只总是4只。不断的增大n_pairs,程序和结果如下:
import random
n_pairs = 100
final = 0
while abs(final - 11) > 0.01:
n_picked = 11 # The number of socks we are going to pick
n_odd = int(n_pairs * 0.4)
# The total number of socks in the laundry
n_socks = n_pairs * 2 + n_odd
socks = [i for i in range(n_pairs)] * 2 + \
[i for i in range(n_pairs, n_pairs + n_odd)]
result = []
for i in xrange(10000):
picked_socks = random.sample(socks, min(n_picked, n_socks))
unique_socks = len(set(picked_socks))
pairs = len(picked_socks) - len(set(picked_socks))
result.append(unique_socks)
final = float(sum(result)) / len(result)
print 'n_pairs:%.f , socks:%.f , result:%.3f ' % (n_pairs, n_socks, final)
n_pairs += 100
从结果看,大约要2600双袜子才能达到预期效果!当然,实际中,单只的数量会随着袜子总量增多而增多。即使我们假设会有40%的遗失(即n_odd = int(n_pairs * 0.4)),那么结果是要1900双袜子, 760只单袜子,共计4560只袜子!!
很显然,这不科学!
3.近似贝叶斯计算
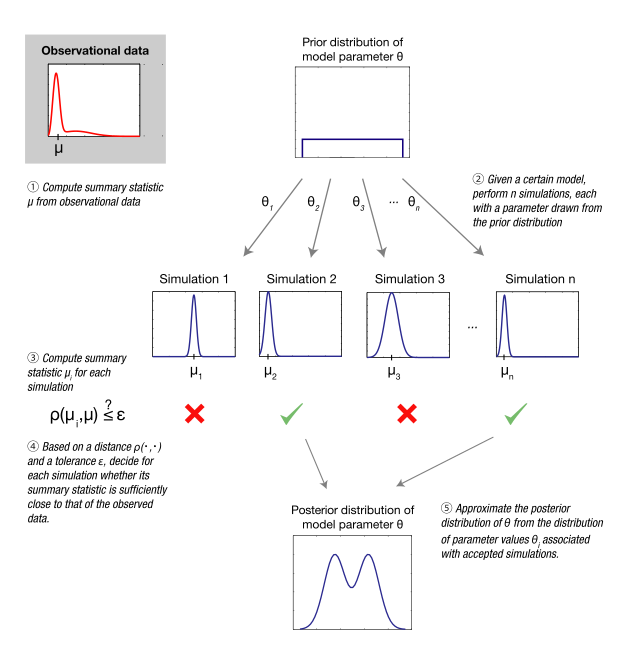
Approximate Bayesian computation(ABC, 近似贝叶斯计算)是贝叶斯统计的基本方法,基本思路如下:
- 1.构建一个生成模型用于生成你的目标数据。这里你需要假设待估计参数的先验分布(可以参考贝叶斯方法生成数据的步骤);
- 2.从先验分布中生成相应的参数(这里称之为试验参数, tentative parameters),并带入生成目标数据的生成模型;
- 3.判断模拟的结果是否符合实际数据。如果符合实际数据,就把该试验参数保存到一个列表中;否则就扔掉;
- 4.大量的重复步骤2、3,就会得到一堆试验参数值;
- 5.最后,得到的这些试验参数值就是参数的后验概率分布。与实际观测越符合的参数值,越容易被保存下来。
3.1选择先验概率
如何选择一个合适的先验概率分布呢?我们的参数是 n_socks(袜子总数), n_pairs(成对的袜子数) 和 n_odd(成单的袜子数)。我们目前所能知道的是这两者都是离散整数。一个比较不错的选择是泊松分布(适合于描述单位时间内随机事件发生的次数),但是泊松分布的期望和方差都是一个参数值。
我们考虑到一个家庭大约3-4人,每人每周换5次袜子,这里选择n_socks服从negative binomial分布,即n_socks = random.negative_binomial(30,0.42),对于n_pairs,不直接使用概率分布,而是考虑n_socks中出现n_pairs的比例,期望是95%,使用beta分布,即random.beta(20,2,1)
3.2程序与结果
import random
from numpy import random as rd
n_picked = 11
result = []
sum_pairs = []
sum_socks = []
for i in xrange(100000):
# n_socks = int(abs(rd.normal(30,15)))
n_socks = rd.negative_binomial(30, 0.42, 1)[0]
n_pairs = int(rd.beta(20, 2, 1) * n_socks / 2.0)
n_odd = n_socks - n_pairs * 2
socks = [i for i in range(n_pairs)] * 2 + \
[i for i in range(n_pairs, n_pairs + n_odd)]
# pick the socks randomly
picked_socks = random.sample(socks, min(n_picked, n_socks))
unique_socks = len(set(picked_socks))
pairs = len(picked_socks) - len(set(picked_socks))
result.append([n_pairs, n_socks, unique_socks])
if unique_socks == 11:
sum_pairs.append(n_pairs)
sum_socks.append(n_socks)
print float(len(sum_pairs)) / 100000
print 'average pairs: ', float(sum(sum_pairs) / len(sum_pairs))
print 'average socks: ',float(sum(sum_socks) / len(sum_socks))
在程序中,n_socks有过不断的调整,按照上面结果得到袜子总数是45只,其中有20双成对的,而实际上袜子总数是45只,21双成对的。但是,这与先验分布的选择关系非常大。不同的参数和先验分布的选择,会导致完全不同的结果!